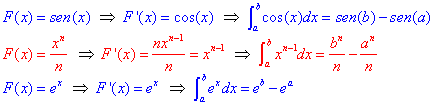
Introducción
De acuerdo con el segundo Teorema Fundamental del Cálculo, toda derivada nos proporciona una fórmula para calcular una integral. Por ejemplo:
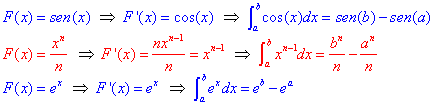
Así que, si deseamos calcular la integral ![]() , nuestra primera reacción será localizar una función
, nuestra primera reacción será localizar una función ![]() tal que
tal que ![]() y entonces el valor de dicha integral sería simplemente
y entonces el valor de dicha integral sería simplemente ![]() . No siempre será fácil encontrar tal función
. No siempre será fácil encontrar tal función ![]() , pero no estará de más intentar este primer camino.
, pero no estará de más intentar este primer camino.
Definición
A una función ![]() que cumpla que
que cumpla que ![]() le llamaremos función primitiva de
le llamaremos función primitiva de ![]() .
.
Una observación
Apoyados en el primer Teorema Fundamental del Cálculo, sabemos que si ![]() es continua, siempre tiene una primitiva, a saber:
es continua, siempre tiene una primitiva, a saber: ![]() . Sin embargo lo que sería deseable es poder expresar tal función primitiva, en términos de funciones conocidas, sean polinomios, trigonométricas, logarítmicas, sus inversas, etc. o mediante operaciones con ellas, incluída la composición. Es decir nos gustaría poder encontrar primitivas en términos de lo que llamaremos funciones elementales.
. Sin embargo lo que sería deseable es poder expresar tal función primitiva, en términos de funciones conocidas, sean polinomios, trigonométricas, logarítmicas, sus inversas, etc. o mediante operaciones con ellas, incluída la composición. Es decir nos gustaría poder encontrar primitivas en términos de lo que llamaremos funciones elementales.
El propósito
Dada la observación anterior, el propósito del tema de Integración que nos ocupa, será desarrollar en lo posible, la teoría necesaria que nos permita establecer métodos para calcular primitivas en términos de funciones elementales.
Habrá funciones que se resistan o que definitivamente sean imposibles. En las primeras la práctica, el conocimiento de los métodos y los artificios algebraicos ayudarán a salir adelante y en las segundas habrá que dar otro tratamiento que será motivo de un trabajo posterior.
Se sabe que por ejemplo, que no existe una función elemental ![]() tal que
tal que ![]() , no obstante que
, no obstante que ![]() es continua en todos los reales. Hay un teorema que lo demuestra, pero por su complejidad, se encuentra fuera de los propósitos de este apartado.
es continua en todos los reales. Hay un teorema que lo demuestra, pero por su complejidad, se encuentra fuera de los propósitos de este apartado.