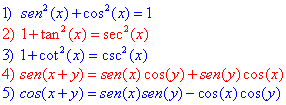
Integración por sustitución trigonométrica

En este apartado seguiremos ejemplificando el método de sustitución, derivado del teorema 2, pero ahora mediante sustituciones con expresiones trigonométricas y para las cuales será necesario tener presentes las identidades trigonométricas siguientes:

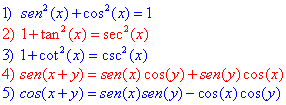
Así como algunas que se obtienen a partir de las anteriores:

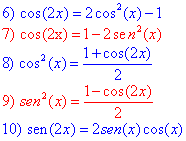
Además también es importante tener presente el teorema 2:

Teorema 2 (Integración por sustitución)

o en esta otra formulación:


Ejemplos

En los ejemplos que presentaremos, seguiremos insistiendo en encontrar las correspondientes sustituciones, sin preocuparnos por los límites de integración.

En los siguientes ejemplos, haremos uso de las identidades trigonométricas
mencionadas arriba y nos referiremos en su aplicación al número que las identifica.

En los siguientes ejemplos, ilustraremos la forma de trabajar integrales de
potencias de funciones trigonométricas. Las identidades trigonométricas son
fundamentales, sobre todo aquellas que reducen las potencias, como las 8) y 9).

En los siguientes ejemplos, ilustraremos cómo abordar casos
generales de integración de potencias de funciones trigonométricas.

En el caso de integrales del tipo: se siguen procedimientos similares ya sea utilizando la identidad 1) para los casos en que n o m sean impares y las identidades 8) o 9) en caso de que n y m sean pares.

En el siguiente apartado, seguiremos con otro método de integración, propio para integrar cocientes de funciones polinomiales.