Continuidad e Integrabilidad

En este apartado encontrarás fundamentalmente el teorema que asegura que toda función continua en un intervalo cerrado [a,b] es integrable sobre [a,b]. Para la demostración de este teorema, necesitamos algunos conceptos y resultados previos sobre continuidad y continuidad uniforme, que también serán incluidos. En realidad, es un teorema fácil de aceptar, pero si gustas formalizarlo, aquí tienes esta sección.

Un teorema de continuidad que debes recordar



Este teorema es la conjunción de uno de los teoremas fuertes de continuidad, el 2 y el teorema 6 del mismo tema, en el curso de Cálculo diferencial e integral I.

Definición

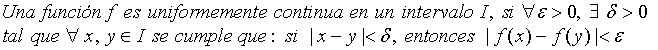
Observaciones

• La continuidad uniforme es una propiedad definida para todo un intervalo, mientras que la continuidad se puede definir en un sólo punto.


• Debe ser claro que una función uniformemente continua en un intervalo I, es continua en tal intervalo I.


• En la continuidad, la depende de y del punto donde desee averiguar, mientras que en la continuidad uniforme, sólo depende de . Es decir, para cada sólo hay que encontrar una que sirva para todo x, y cuya distancia entre ellos, sea menor que delta.

Lema 2 (continuidad uniforme en intervalos cerrados consecutivos)

Lema 3 (Continuidad en [a,b] => continuidad uniforme en [a,b])

Teorema 3 (continuidad en [a,b] => integrabilidad en [a,b])

Con este teorema, tenemos un conjunto mucho muy grande de funciones integrables, particularmente todas las polinomiales.