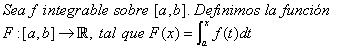
Por el Teorema 4, sabemos que esta función está bien definida, puesto que si f es integrable sobre todo [a,b], entonces f es integrable sobre cualquiera subintervalo [a,x], para todo x en [a,b].
La integral como una función
En este apartado iniciarás el estudio de la integral como una función, lo cual te permitirá conectarla con los conceptos ya estudiados de límite, continuidad y derivada. Es decir, podrás estudiar la continuidad de una función integral, aplicarle límite y obtener su derivada.
Definición
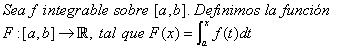
Por el Teorema 4, sabemos que esta función está bien definida, puesto que si f es integrable sobre todo [a,b], entonces f es integrable sobre cualquiera subintervalo [a,x], para todo x en [a,b].
Para la demostración del siguiente teorema, será necesario que recuerdes que:
Si f es integrable sobre [a,b], entonces f está acotada en [a,b]
Esta propiedad de la integral como una función es interesante y se cumple, aun que la función f sea discontinua, como podrás apreciar en los siguientes ejemplos.