Conceptos preliminares
En este apartado haremos ver la necesidad de trabajar con mayor formalidad los conceptos de logaritmo y exponencial, con la finalidad de poder demostrar propiedades conocidas y poderlas aplicar con la conciencia tranquila.
Los exponentes
En los cursos elementales de matemáticas se da por hecho la siguiente ley de los exponentes,
cuando mucho se ilustra de la siguiente manera para el caso de exponentes naturales:
De donde, si se quiere mantener la ley de los exponentes para el caso n=0, se obtiene que: 
. Lo cual obliga a definir: 
.
Igualmente, si se desea mantener la ley de los exponentes, al caso de los enteros negativos, se tendría que:
, lo cual obliga a definir: 
.
Con esta misma idea, mantener la ley de exponentes para potencias racionales, implicaría que: 
, lo cual obliga a definir: 
. Y entonces, basta definir 
.
Hasta ahí se llega generalmente, pero ¿Qué pasaría si tuviésemos un exponente irracional? Por ejemplo, cómo interpretar 
?. En todos los casos anteriores se podía contar "tantas veces". Aun más, ¿Cómo hacer ver la ley de exponentes para estos casos?
Los logaritmos
De manera similar en los cursos de matemáticas elementales, frecuentemente encontramos una presentación del concepto de logaritmo, de la siguiente manera:
El logaritmo de un número b, en una base a positiva dada, es el exponente x, al cual se debe elevar a, para obtener b.
Es decir:
Así por ejemplo |
O también |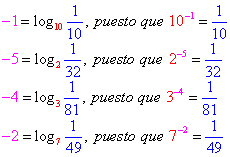
|
O inclusive
 |
|
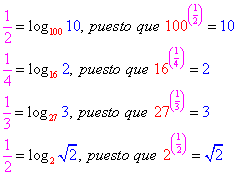Es decir, 
. Sin embargo, bastaría preguntar por 
. O bien, ¿Cuánto vale x, tal que 
?.
Conclusiones
.
