En busca de la exponencial

En este apartado buscaremos construir la función exponencial, definida en todos los reales. Lo hacemos pensando fundamentalmente en que ésta cumpla la ley de los exponentes:

desde luego para a > 0. Además, con la experiencia de la definición hasta los racionales vimos que:

es decir, logaritmo y exponencial son inversa una de la otra.

Iniciamos la búsqueda

Buscamos una función f derivable, que no sea idénticamente cero, que satisfaga la ley de los exponentes y que tenga inversa, es decir:

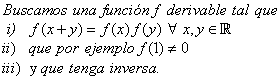
La propiedad i) garantiza que f cumpla la ley de los exponentes y la ii) garantiza que no sea idénticamente cero. La buscamos derivable para poder recurrir a su derivada y obtener información de ella. Recordemos que la derivada de una función nos aporta conocimiento sobre la propia función.

Recurrimos a su derivada

Con las propiedades anteriores, tenemos que:

(1)

Pero por otra parte

(2)

Luego entonces sustituyendo (2) en (1), queda que:

(3)

Suponiendo que el límite en (3) existe, le llamaremos k y sustituyendo en (1), nos quedaría finalmente que:

(4)

Aunque pudiésemos calcular el valor de k en (4), de cualquier manera llegamos a una expresión donde la derivada de f, depende de f y ésta última es la que queremos encontrar. Necesitamos explorar otro camino y para ello, aplicaremos iii), es decir recurriendo al hecho de que f tiene inversa.

Ahora recurrimos a su inversa

Antes de empezar la nueva exploración, sera importante que recuerdes la expresión para la derivada de la inversa, si no la recuerdas puedes dar clic en Lema 1. También es importante que recuerdes el corolario del primer teorema fundamental del cálculo, igualmente, si no lo recuerdas puedes dar clic en Corolario.

Para ser consistente con lo desarrollado hasta los racionales, llamaremos , así tendríamos que:

De aquí, por el corolario del primer teorema fundamental, tenemos que

,

pero como

,

entonces nos queda que

(5)

En la expresión (5) seguimos con el problema del valor de k. Una manera de salvar el problema, es declarar k=1 y definir

confiando en que se trata del logaritmo de x en alguna base que no conocemos por ahora.

Conclusión

• Buscando cómo definir la función exponencial f, con base a, llegamos a la definición de su inversa, log(x), en una base aun no conocida, pero que podremos calcular más adelante.


• Lo importante es que ya tenemos una definición que además se cumple para toda x > 0 y que con ella volveremos a buscar la exponencial.

 

---