La función exponencial

En este apartado encontrarás la definición de la función exponencial y la demostración de sus propiedades más importantes. Aprovecharemos la idea de que, al menos hasta los racionales, logaritmo y exponencial son inversas una de la otra. Tomamos esta idea y definimos la función exponencial, que denotaremos por exp, de la siguiente manera:

Definición de la función exponencial

Para analizar su gráfica, veamos el siguiente teorema sobre su derivada. Para su demostración sera importante que recuerdes la la derivada del logaritmo y la expresión para la derivada de la inversa, si no la recuerdas puedes dar clic Lema 1.

Teorema 2

Es decir, la derivada de la exponencial en cada punto, es igual a su propio valor en tal punto. Se sabe que a excepción de la función constante cero, la exponencial es la única con la propiedad establecida en el Teorema 2.

Primer análisis de exp(x)

1. 
   
   
2. 
   
   
3. 
   
   
4. , puesto que:
   
   
   
5. Aún más, , puesto que la función , sólo tiene un mínimo local en x = 0. ¿Puedes comprobarlo?. Recuerda los criterios de la primera y segunda derivada.

Basados en la propiedad del logaritmo, establecida en el Teorema 1 y del hecho que las funciones log y exp son inversas entre sí, demostraremos una de las propiedades más importantes de la función exponencial, a saber:

Teorema 3

Esta función exp, ya cumple los requisitos de la función cuya búsqueda emprendimos en el apartado 2 de este tema ¿Recuerdas?:

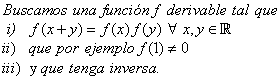
El teorema 3, demuestra que satisface el inciso i).
Respecto a ii), sabemos que y por último cumple iii), es decir, tiene inversa.

El número exp(1) será motivo de análisis en el siguiente apartado. Por ahora buscaremos graficar la función exponencial, relacionada con la gráfica de su inversa, log.