Otros resultados
En este apartado encontrarás otros resultados sobre la función exponencial, entre ellos su relación con cualquier función polinomial.
De antemano, como lo vimos en el teorema 2, sabemos que: ![]() . Queremos saber si el recíproco del teorema 2 es cierto. Veamos entonces el siguiente teorema.
. Queremos saber si el recíproco del teorema 2 es cierto. Veamos entonces el siguiente teorema.
Además de las propiedades demostradas en los teoremas 2 y 3, la función exponencial tiene otra súmamente importante: "La función exponencial exponencial crece más rápidamente que cualquier polinomio". Este resultado lo demostraremos en el Teorema 6, pero antes veamos otro resultado que necesitaremos:
A partir de este resultado se facilita analizar un cierto tipo de funciones, tales que sus derivadas de cualquier orden, en un punto, permanecen igual a cero, como por ejemplo:
![]()
 , estaremos seguros que esta nueva función es continua en cero.
, estaremos seguros que esta nueva función es continua en cero. y
y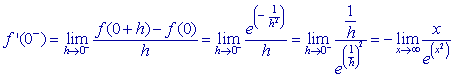

 donde
donde 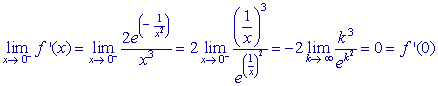 donde
donde 

Una situación similar ocurre con la función: 
Es decir, se trata de una función extremadamente plana alrededor del origen y tal que ![]() . Observa su gráfica y las de la primera y segunda derivadas.
. Observa su gráfica y las de la primera y segunda derivadas.