Conceptos previos

En este apartado podrás encontrar las recomendaciones de los conceptos previos que debes revisar, antes de abordar el tema del Teorema Fundamental del Cálculo.

Debes tener clara la definición de la integral como una función. ¿Recuerdas?

Definición

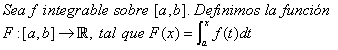
Debes recordar el Teorema 4 (Aditividad de la integral en intervalos consecutivos), de la sección de Integrales, en su apartado de Algebra de funciones integrables. Por este teorema, sabemos que la función integral está bien definida, puesto que si f es integrable sobre todo [a,b], entonces f es integrable sobre cualquiera subintervalo [a,x], para todo x en [a,b].

También debes recordar el Teorema 7 (Acotación de la integral) de la sección de Integrales, en su apartado de Algebra de funciones integrables. Este teorema en particular, se utilizará en la demostración del primer teorema fundamental de cálculo. Te ahorrarás mucho tiempo si lo revisas antes de pasar al siguiente apartado.

Además, debes tener bien presente el Teorema 8 de la sección de Integrales, que afirma la continuidad de F en [a,b], si f es integrable en [a,b].

Otro resultado que te será muy necesario es el Teorema del valor medio para derivadas. ¿Lo recuerdas?. Lo puedes encontrar en el primer curso de Cálculo Interactivo en la sección de Derivadas, Teoremas importantes I, Teorema 4. Este teorema en particular, se utiliza para demostrar el segundo teorema fundamental de cálculo, así que es importante que lo revises.

Algo más que sería importante que recordaras, es la Regla de la cadena para derivar una composición de funciones. Basta con que recuerdes que: y que puedas reconocer las componentes de una función compuesta. Por ejemplo, ¿cómo escribirías las componentes de la siguiente función?

Si no recuerdas, debes revisar estos conceptos en tu libro, en el tema de funciones del primer curso de Cálculo Interactivo o dar clic aquí.

Evidentemente hay más resultados que serán necesarios, pero éstos son cruciales.